오늘 포스팅할 논문은 "Debiased Self-Training for Semi-Supervised Learning'입니다.
이 논문은 NeurIPS 2022 Oral Paper로 채택되었습니다.
자세한 코드 정보는 저자들이 공유한 Github에서 확인하세요!
Key Words
- Training Bias: The bias increment brought by some unreasonable training strategies
- Data Bias: The bias inherent in semi-supervised learning tasks, such as sampling bias and pretrained representation of the unlabeled data.
이 논문은 위의 두 핵심 단어를 가지고 서술합니다.
Contribution
- Systematically identify the problem and analyze the causes of self-training bias in semi-supervised learning.
- Propose DST, a novel approach to mitigate the self-training bias and boost the stability and performance balance across classes, which can be used as a universal add-on for mainstream self-training methods.
- Conduct extensive experiments and validate that DST achieves an average boost of 6.3% against state-of-the-art methods on standard datasets and 18.9% against FixMatch on 13 diverse tasks.
Weakness of Pseudo Label
이 논문에서는 pseudo label의 약점을 언급합니다.
가령, 모델이 한쪽으로 overfitting 되어 bias를 가지게 된다면 pseudo label을 생성할 때에서 bias가 적용되게 됩니다.
Bias를 가지고 있는 모델로 pseudo label을 생성했기 때문에 pseudo label 또한 bias를 가지고 있습니다.
Pseudo Label를 통해 unlabeled dataset을 활용 및 학습을 한다면 psuedo label의 bias로 인해서 model의 bias가 축적되는 문제를 언급합니다.
이러한 문제점들을 극복하기 위해서 더 좋은 pseudo label을 생성하거나 잘못된 pseudo label에 대해서 강건한 모델을 만들기 위한 여러 시도들이 있습니다.
Generate higher-quality pseudo labels
MixMatch, ReMixMatch, UDA, Fixmatch, FlexMatch 등의 여러 유명 논문들은 더 좋은 pseudo label을 생성하기 위한 여러 대안을 제시합니다.
이 논문에서는 위의 논문들과의 차이점으로 다음을 이야기합니다.
'Different from the above methods that manually design specific criteria to improve the quality of pseudo labels, we estimate the worst case of self-training bias and adversarially optimize the representations to improve the quality of pseudo labels automatically'
Improve tolerance to inaccurate pseudo labels
대표적으로 Temporal Ensembling, Mean Teacher, Noisy Student, Co-training, MMT, DivideMix 등을 언급하고 있습니다.
위의 방법론들은 model의 pseudo label header의 weight가 공유되기 때문에 잠재적으로 잘못된 pseudo label을 통한 학습의 위험성이 있다고 설명합니다.
하지만 이 논문은 pseudo label header가 절대 unlabeled dataset으로부터 학습되지 않기 때문에 부정확한 pseudo label로부터 더 자유롭다고 설명합니다.
'In these methods, each classifier head is still trained with potentially incorrect pseudo labels generated by other heads. In contrast, in our method, the classifier head that generates pseudo labels is never trained with pseudo labels, leading to better tolerance to inaccurate pseudo labels'

Training with pseudo labels aggressively in turn enlarges the self-training bias on some categories.
논문에서는 FixMatch를 통해 Training bias를 설명합니다.
lebeled dataset 만을 가지고 Supervised learning을 통해 학습했을 때 보다 FixMatch로 학습했을 때 Class별 오차의 폭이 증가된 것을 알 수 있다고 말합니다.
그리고 이 논문에서 제시하는 DST$($Debias Self-Training$)$을 사용하면 이러한 오차의 폭을 줄일 수 있다고 설명합니다.

Debiased Self-Training
Labeled Dataset: $\mathscr{L}=\left\{(X^{l}_{i}, y^{l}_{i}) \right\}^{n_l}_{i=1}$ of $n_{l}$ labeled samples
Unlabeled Dataset: $\mathscr{U}=\left\{(X^{u}_{j}) \right\}^{n_u}_{j=1}$ of $n_{u}$ unlabeled samples
여기서 $n_{l} \ll n_{u}$
$\psi$: feature generator
$\alpha$: task-specific header
The Standard cross-entropy loss on weakly augmented labeled: $L_{\mathscr {L}}(\psi, h)=\frac {1}{n_{l}}\sum_{i=1}^{n_{l}}L_{CE}((h\circ \psi \circ \alpha))(X^{l}_{i}, y^{l}_{i})$
FixMatch에서 사용하는 weakly augmented unlabeled dataset에 대한 prediction: $\hat{\textbf{p}}=(h\circ\psi\circ\alpha)(\textbf{x})$
pseudo labeling function: $\hat {f}_{\psi, h}$
아무튼 이전 포스팅과 동일하게 unlabeled에 대한 loss term은 아래와 같다.
$L_{\mathscr {U}}(\psi, h, \hat {f})=\frac {1}{n_{u}}\sum_{j=1}^{n_{u}}L_{CE}((h\circ \psi \circ \mathcal {A})(X^{u}_{j}) ), \hat {f}(\textbf {x}_{u}^{j}))$
그래서 이 논문에서 표기하는 FixMatch의 optimization objective는 $\underset {\psi, h}{\text{min}} \space L_{\mathscr{L}}(\psi h) +\lambda L_{\mathscr{U}}(\psi, h, \hat{f}_{\psi, h}))$
Handle Training Bias by Different Header
그런데 앞에서 언급했던바와 같이 FixMatch와 같이 pseudo label을 사용하면 pseudo label로 인해 bias가 누적이 됩니다.
그래서 이 논문에서는 pseudo label을 생성하는 header는 labeled dataset만으로 학습합니다. 그래서 기존 FixMatch의 optimization objective에서 약간 변형되어 아래와 같이 정리됩니다.
$\underset{\psi, h, h_{pseudo}}{\text {min}} \space L_{\mathscr {L}}(\psi, h) +\lambda L_{\mathscr {U}}(\psi, h_{pseudo}, \hat {f}_{\psi, h}))$
Handle Data Bias by Expecting Worst Case
위의 변형된 optimization objective를 통해서 training bias를 어느 정도 개선했다고 볼 수 있습니다. 하지만 여전히 data bias가 남아있기 때문에 이 부분에 대해서 고민해야 합니다. Data bias를 해결하지 않는다면 실제 decision boundary와는 다르게 특정 data sample에 bias 한 decision boundary를 학습하게 됩니다. 이를 논문의 figure 6에서 시각화해 보여주고 있습니다.
그런데 문제는 unlabeled dataset은 label 정보가 없으니까 어떤 class에 대해서 얼마만큼 bias를 가지고 있는지 측정할 수 없다는 점입니다. 그래서 논문에서는 training bias를 학습 방법에 따른 pseudo label의 잘못된 활용으로 data bias의 축적으로 이야기하고 있습니다. 즉, training bias는 data bias의 누적!
그래서 이 논문에서 말하고 있는 Worst Case는 labeled data에 대해서는 모두 올바르게 예측하지만, pseudo label은 모두 잘못된 label로 생성해서 계속 학습하는 case입니다. 이를 수식으로 표현하자면 다음과 같습니다.
$h_{worst}(\psi) = \underset {h'}{\text {arg max}} \space L_{\mathscr {U}}(\psi, h', \hat {f}_{\psi, h}) - L_{\mathscr {L}}(\psi, h')$
그래서 worst case로부터 가급적 멀리 decision boundary를 생성하기 위해서 아래와 같은 optimization objective를 제시합니다.
$\underset {\psi}{\text {min}}\space L_{\mathscr {U}}(\psi, h_{worst}(\psi)), \hat {f}_{\psi, h}) - L_{\mathscr {L}}(\psi, h_{worst}(\psi)$
Overall Loss Term
해당 논문에서 제시하고 있는 DST의 최종 loss term은 아래와 같습니다.
$\underset {\psi, h, h_{pseudo}}{\text {min}} \underset {h'}{\text {max}} \space L_{\mathscr {L}}(\psi, h) + L_{\mathscr{U}}(\psi, h_{pseudo}, \hat{f}_{\psi,h}) +(L_{\mathscr{U}}(\psi, h', \hat{f}_{\psi, h}) - L_{\mathscr{L}}(\psi, h'))$
Experiments
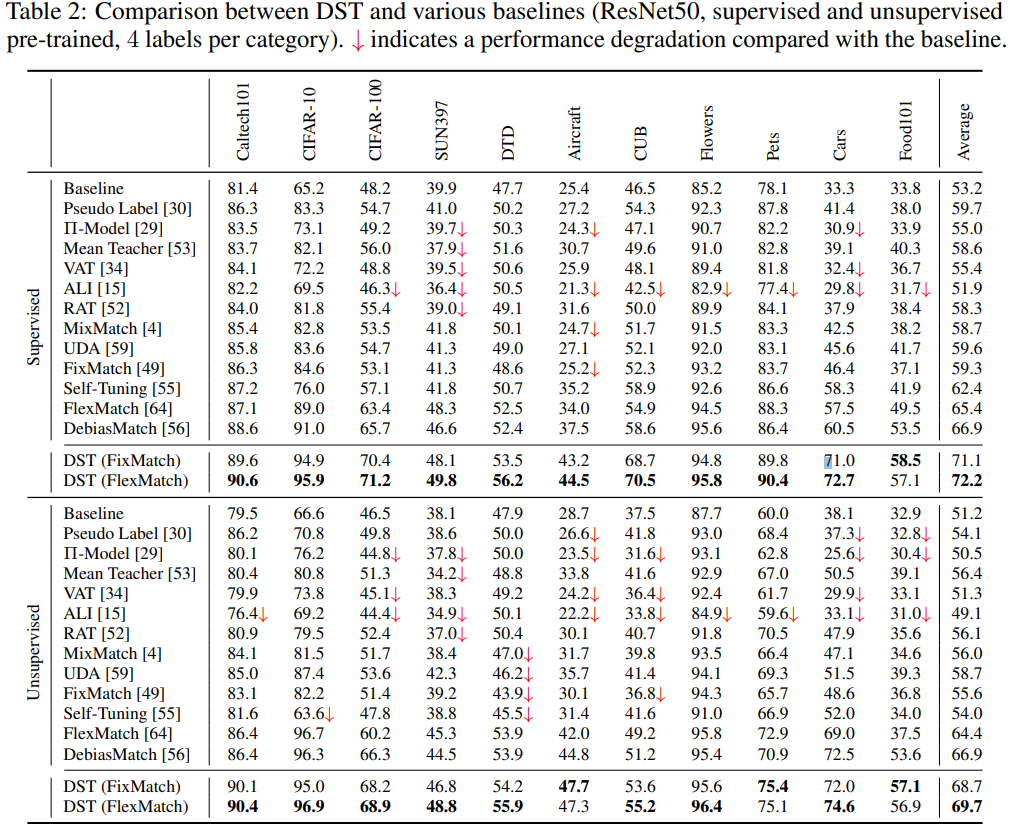
논문에서는 정말 많은 방법론에 대해서 실험을 진행했고, appendix에도 정리를 해놓았습니다.
그래서 논문의 Table 2만 첨부하도록 하겠습니다. 자세한 실험 내용은 논문을 통해 확인해 주세요!