Link: https://arxiv.org/pdf/2404.14109
Summary
- $\mathcal{L}_{\text{intra}} = \frac{1}{n} \sum{i=0}^{n} d\left( t_i, s_i \right)$
- 위 수식에서 $t_i$와 $s_i$가 가깝도록 학습을 하게 되는데, 이게 $d\left( t_i, s_i \right) < d\left( t_j, s_i \right)$를 보장하지 못한다는 문제가 있음을 지적
- Loss가 0이더라도 student가 teacher의 내부 표현의 구조나 결정 경계를 배움에는 한계가 있다.
- Teacher’s raw score before softmax: [0.4, 0.4], [0.6, 0.6] → [0.5, 0.5], [0.5, 0.5]
- Student’s raw score before softmax: [1.4, 1.4], [5.6, 5.6] → [0.5, 0.5], [0.5, 0.5]
- 모두 loss는 0
CKD의 핵심은 샘플 단위 정렬(sample-wise alignment) 문제
Assumption
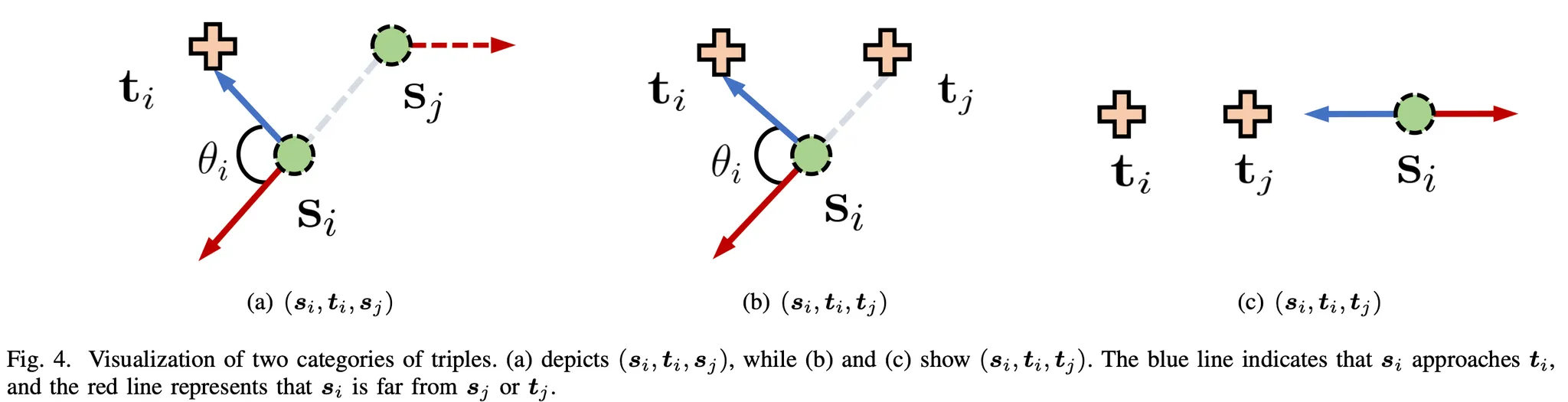
- Teacher is fixed
- (c) is worst case in KD
- (a)의 경우에도 $S_j$가 $\vec{S_it_i}$ 위에 있을 때 (c)와 같은 문제가 생기지만 $S_j$는 update 되기 때문에 학습에 따라 문제가 완화됨
- 그래서 저자는 (a)의 방식을 선택
Proposed Method
CKD의 핵심은 sample-wise alignment
- $\mathcal{L}_{\text{total}} = \mathcal{L}_{\text{intra}} + \mathcal{L}_{\text{inter}}$
- $\mathcal{L}_{\text{intra}} = \frac{1}{n} \sum\limits_{i=0}^{n} d\bigl(t_i, s_i\bigr)$
- $\mathcal{L}_{\text{inter}} = -\frac{1}{n (n-1)} \sum\limits_{i=0}^{n} \sum\limits_{\substack{j=0 \\ j \neq i}}^{n} d(s_i, s_j)$
KD and Contrastive
$\mathcal{L}{\text{KD}} = \mathbb{E}{x_i \sim \mathcal{X}} d\left(t_i, s_i\right) - \beta \, \mathbb{E}{x_i \sim \mathcal{X}} \, \mathbb{E}{x_j \sim \mathcal{X}} d\left(s_i, s_j\right)$
$\quad\quad~~ = \mathbb{E}{x_i \sim \mathcal{X}} \left[ - \left( f\left( t_i, s_i \right) - \beta \, \mathbb{E}{x_j \sim \mathcal{X}} f\left( s_i, s_j \right) \right) \right]$
$\quad\quad~~= \mathbb{E}{x_i \sim \mathcal{X}} \ln \left[ \frac{\mathbb{E}{x_j \sim \mathcal{X}} e^{\beta f\left( s_i, s_j \right)}}{e^{f\left( t_i, s_i \right)}} + \frac{e^{f\left( t_i, s_i \right)}}{e^{f\left( t_i, s_i \right)}} - 1 \right]$
$\quad\quad~~\simeq \mathbb{E}{x_i \sim \mathcal{X}} \left[ - \ln \frac{e^{f\left( t_i, s_i \right)}}{e^{f\left( t_i, s_i \right)} + \mathbb{E}{x_j \sim \mathcal{X}} e^{\beta f\left( s_i, s_j \right)}} \right]$
$\quad\quad~~\simeq \mathbb{E}{x_i \sim \mathcal{X}} \left[ - \ln \frac{e^{f\left( t_i, s_i \right)/\tau}}{e^{f\left( t_i, s_i \right)/\tau} + \mathbb{E}_{x_j \sim \mathcal{X}} e^{\beta f\left( s_i, s_j \right)/\tau}} \right]$
Experimental Results

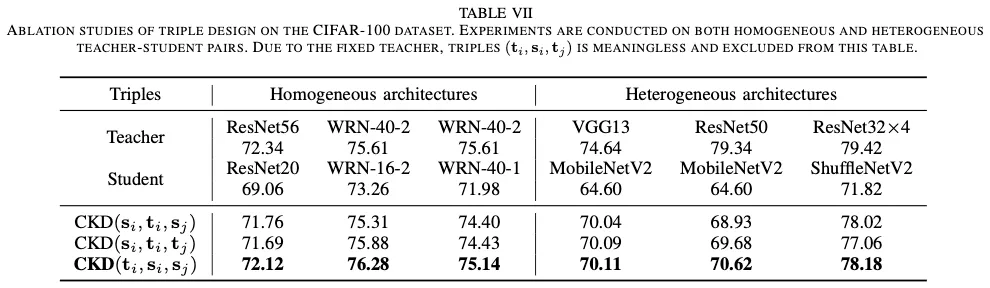
Opinion
- positive와 negative sample을 어떻게 설정하냐에 따라 목적 및 성능이 다름 정도만 가져가면 될 것 같다.
