Relation DETR: Exploring Explicit Position Relation Prior for Object Detection

ECCV 2024 Accepted Paper.

Link: https://arxiv.org/pdf/2407.11699 

 

Summary

• suggesting that it arises from the self-attention that introduces no structural bias over inputs
• introduces an encoder to construct position relation embeddings for progressive attention refinement
  • further extends the traditional streaming pipeline of DETR into a contrastive relation pipeline to address the conflicts between non-duplicate predictions and positive supervision.
• introduce a class-agnostic detection dataset, SA-Det-100k

Introduction or Motivation

Background

• Despite exhibiting impressive detection performance on large-scale datasets such as COCO, their performances are prone to be influenced by dataset scale and suffer from slow convergence.
• Negative predictions dominates the majority of the loss function, causing insufficient positive supervision.
• Therefore, more samples and iterations are required for convergence.
• Despite these advancements $($DINO, DN-DETR, H-DERTR, etc.$)$, there has been little exploration of the issue from the perspective of self-attention, which is widely used in the transformer decoders in most DETR detectors.

Motivation

• Effectiveness of Self-Attention
  • Establishes high-dimensional relation representations among sequence embeddings.
  • Key for modeling relations among different detection feature representations.
• Limitations
  • Relations are implicit with no structural bias over inputs.
  • Requires learning positional information from training data.
  • Learning process is data-intensive and slow to converge.
• Motivation for Improvement
  • Introduce task-specific bias.
  • Aim for faster convergence.
  • Reduce dependence on large amounts of training data.

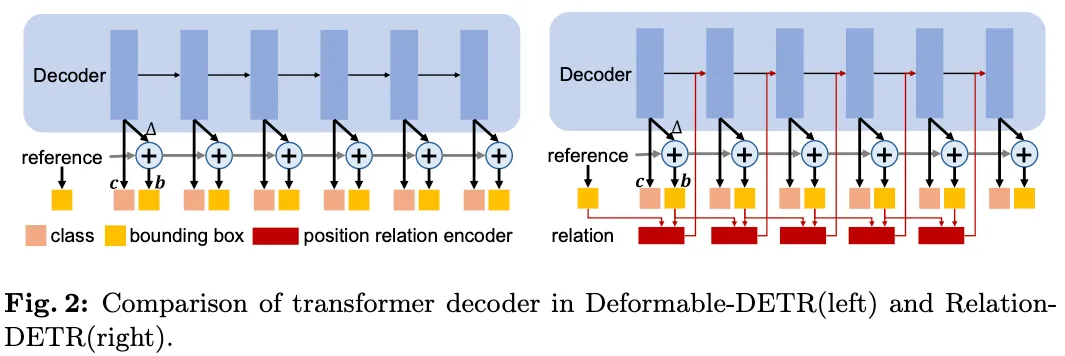
Compared to previous works, the main feature of Relation-DETR is the inte- gration of explicit position relation. In contrast, prior works focus on implicitly learned attention weights from training data, leading to slow convergence.

 

Method

• a position relation encoder for progressive attention refinement
• the streaming pipeline of DETR into a contrast pipeline
  • to emphasize the influence of position relation on removing duplication while maintaining sufficient positive supervision for faster convergence.

Position relation encoder

• Directly construct instance-level relation through a simple position encoder, maintaining an end-to-end design for DETR.
• our position relation encoder represents the high-dimensional relation embedding as an explicit prior for self- attention in the transformer.
• This embedding is calculated based on the predicted bounding boxes (denoted as b = [x, y, w, h]) from each decoder layer.
• To ensure that the relation is invariant to translation and scale transformations, we encode it based on normalized relative geometry features:
  • $e(b_i, b_j) = \left[ \log\left(\frac{|x_i - x_j|}{w_i} + 1\right), \log\left(\frac{|y_i - y_j|}{h_i} + 1\right), \log\left(\frac{w_i}{w_j}\right), \log\left(\frac{h_i}{h_j}\right) \right]$
    • BBox WH로 normalization을 해주면 크기에 상관없이 scale bias를 없앰으로써 다른 크기의 object에 대해서 일정한 성능 향상에 유리하다.
• our position relation is unbiased, as $e(b_i,b_j)=0$ when $i = j$.
• relation matrix $E \in \mathbb{R}^{N\times N \times 4}$is further transformed into high-dimensional embeddings through sine-cosine encoding
  • $\text{E}(i,j)=e(b_i, b_j)$
  • $\text{Embed}(\mathbf{E}, 2k) = \sin\left(\frac{s\mathbf{E}}{T^{2k/d_\text{re}}}\right)$
  • $\text{Embed}(\mathbf{E}, 2k+1) = \cos\left(\frac{s\mathbf{E}}{T^{2k/d_\text{re}}}\right)$
• the embedding undergoes a linear transformation to obtain M scalar weights, where M denotes the number of attention heads.
  • $\text{Rel}(\mathbf{b}, \mathbf{b}) = \max\left(\epsilon, W \, \text{Embed}(\mathbf{b}, \mathbf{b}) + \mathbf{B}\right)$
  • $\text{Rel}(\mathbf{b}, \mathbf{b}) \in \mathbb{R}^{N \times N \times M}$

Progressive attention refinement with position relation

 

• $\text{Attn}{\text{Self}}(\mathbf{Q}^l) = \text{Softmax} \left( \text{Rel}(\mathbf{b}^{l-1}, \mathbf{b}^l) + \frac{\text{Que}(\mathbf{Q}^l) \text{Key}(\mathbf{Q}^l)^\top}{\sqrt{d\text{model}}} \right) \text{Val}(\mathbf{Q}^l)$
• $\mathbf{Q}^{l+1} = \text{FFN}\left( \mathbf{Q}^l + \text{Attn}{\text{cross}} \left( \text{Attn}{\text{Self}}(\mathbf{Q}^l), \text{Key}(\mathbf{Z}), \text{Val}(\mathbf{Z}) \right) \right)$
• $\mathbf{b}^{l+1} = \text{MLP}(\mathbf{Q}^{l+1}), \quad \mathbf{c}^{l+1} = \text{Linear}(\mathbf{Q}^{l+1})$

Contrast relation pipeline

 

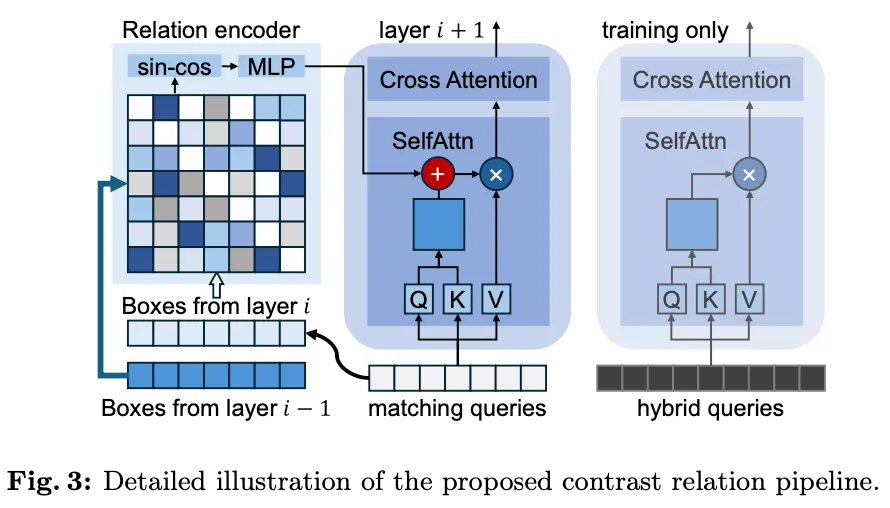
• integrating the position relation among queries in self-attention contributes to non-duplicated predictions in object detection
• construct two parallel sets of queries
  • $\mathbf{Q}_m$: matching queries
  • $\mathbf{Q}_h$: hybrid queries
• The matching queries are processed with self-attention in- corporating position relation to produce non-duplicated predictions:
  • $\text{Attn}_{\text{Self}}(\mathbf{Q}_m^l) = \text{Softmax} \left( \text{Rel}(\mathbf{b}^{l-1}, \mathbf{b}^l) + \frac{\text{Que}(\mathbf{Q}_m)\text{Key}(\mathbf{Q}m)^\top}{\sqrt{d{\text{model}}}} \right) \text{Val}(\mathbf{Q}_m)$
  • $\mathcal{L}_m(\mathbf{p}_m, \mathbf{g}) = \sum{l=1}^{L} \mathcal{L}{\text{Hungarian}}(\mathbf{p}_m^l, \mathbf{g})$
• the hybrid queries are decoded by the same decoder but skip the calculation of position relation to explore more potential candidates.
  • $\text{Attn}_{\text{Self}}(\mathbf{Q}_h^l) = \text{Softmax} \left( \frac{\text{Que}(\mathbf{Q}_h)\text{Key}(\mathbf{Q}_h)^\top}{\sqrt{d{\text{model}}}} \right) \text{Val}(\mathbf{Q}_h)$
  • $\mathcal{L}_h(\mathbf{p}_h, \mathbf{g}) = \sum{l=1}^{L} \mathcal{L}{\text{Hungarian}}(\mathbf{p}_h^l, \tilde{\mathbf{g}})$
    • $\tilde{\mathbf{g}}=\{\mathbf{g}^1, \mathbf{g}^2, \cdots, \mathbf{g}^K\}$: H-DETR’s repeated GT set

Experiment