Self-Supervised Representation Learning with Meta Comprehensive Regularization

AAAI 2024 Accepted Paper

Link: https://arxiv.org/pdf/2403.01549

 

 

Summary

• augmentation을 하면 downstream task에 필요한 정보가 손실이 될 수도 있다.
• 그렇기 때문에 comprehensive representation을 학습할 수 있도록 해야한다.
• 최대한 많은 semantic information을 담아내는 representation을 얻기 위해서 information theory 관점상 Entropy를 최대화 하는 방향으로 가야한다.
• 두 loss의 목적은 비슷: 표현을 풍부하게 만들어 downstream task 성능 향상 하지만 적용 위치가 다름
  • $L_{\text{comp}}$: backbone에서 추출되는 전체 표현의 엔트로피를 높임.
  • $L_{\text{mcr}}$: projection header에서 augmented view 간 meta information 조절, 유사성 & 엔트로피를 함께 유지.
• 결과적으로 backbone이 “포괄적 표현”을 형성, header는 “증강 뷰 간 불변 특성”을 학습시켜 SSL 목표를 달성합니다.
• 이렇게 이중 최적화나 두 단계 학습으로 나눠서 최적화하면 얻을 수 있는 장점:
  1. “augmented view가 서로 닮도록 하는” 과정과
  2. “표현 전체를 풍부하게 유지하는” 과정을 서로 간섭 없이(혹은 적절한 균형으로) 진행할 수 있다

Method

• Comprehensive Representation if and only if $I(z;T)=H(T)$
  • $H(T) \ge \{I(x_1;T, I(x_2, T)\} \ge I(x_1;x_2;T)$
  • $H(T) \ge \{I(z_1;T, I(z_2, T)\} \ge I(z_1;z_2;T)$
    • $x_1, x_2$: augmentated samples within original sample space
    • $z_1, z_2$: augmentated samples within the feature space
  • Augmentation을 하면 Downsteam Task 수행에 필요한 정보가 손실될 수 있다.
  • $\{I(z_1; T), I(z_2;T)\} = I(z_1) \cup I(z_2) \ge I(z_1;z_2, T) = I(z_1;T) \cap I(z_2;T)$
  • Augmented representation이 원본의 포괄적 정보를 얼마나 잘 보존하는지가 Downstream task에 중요한 영향을 준다
• CompMod
  • Address the issue of semantic loss resulting from data augmentation
  • learns a more comprehensive representation and helps facilitate model learning
  • $\hat{h}_{i} :=h^1_i \oplus h^2_i \in \mathbb{R}^{2d}$ : feature fusion like concaternate
  • $\hat{z}i = g{\xi}(\hat{h}_i) \in \mathbb{R}^{d}$
  • but just simple fusion does not guarantee that the learned features encompass all semantics
  • $\mathcal{L}{comp}(\hat{\mathbf{Z}}) = -\text{Tr} \left( \mu \sum{k=1}^{m} \frac{(-1)^{k+1}}{k} (\lambda \hat{\mathbf{Z}} \hat{\mathbf{Z}}^T)^k \right)$
    • $\log \det(I+A)$ 또는 $\log(1+x)$ 형태를 테일러 급수로 전개할 때 $\sum\limits_{k=1}^{\infty} \frac{(-1)^{k+1}}{k} A^{k}$와 같이 표현
    • 의미: 최종적으로 획득된 representation $\hat{Z}$ 자체가 풍부한 semantic information을 가져야한다
      • generalizable representation should be the one with the maximum entropy among all possible representations
      • Inspired by the maximum entropy principle in information theory,
      • corresponding to the maximization of the semantic information associated with the true label.
  • $\mathcal{L}_{mcr}(\mathbf{Z}1, \mathbf{Z}2) = -\sum{t=1}^{2} \text{Tr} \left( \mu \sum{k=1}^{m} \frac{(-1)^{k+1}}{k} (\lambda \hat{\mathbf{Z}} \mathbf{Z}_t^T)^k \right)$
    • 의미: augmented view $\hat{Z}_{t}$도 comprehensive representation에 가까워 지도록 constrains
      • use the comprehensive representation to guide the learning of the backbone network.
      • To enhance the semantic richness of the representation in each augmented view
      • constrain the information contained in the augmented embeddings $Z_1 , Z_2$ to equal the information contained in the comprehensive embedding $\hat{Z}$.

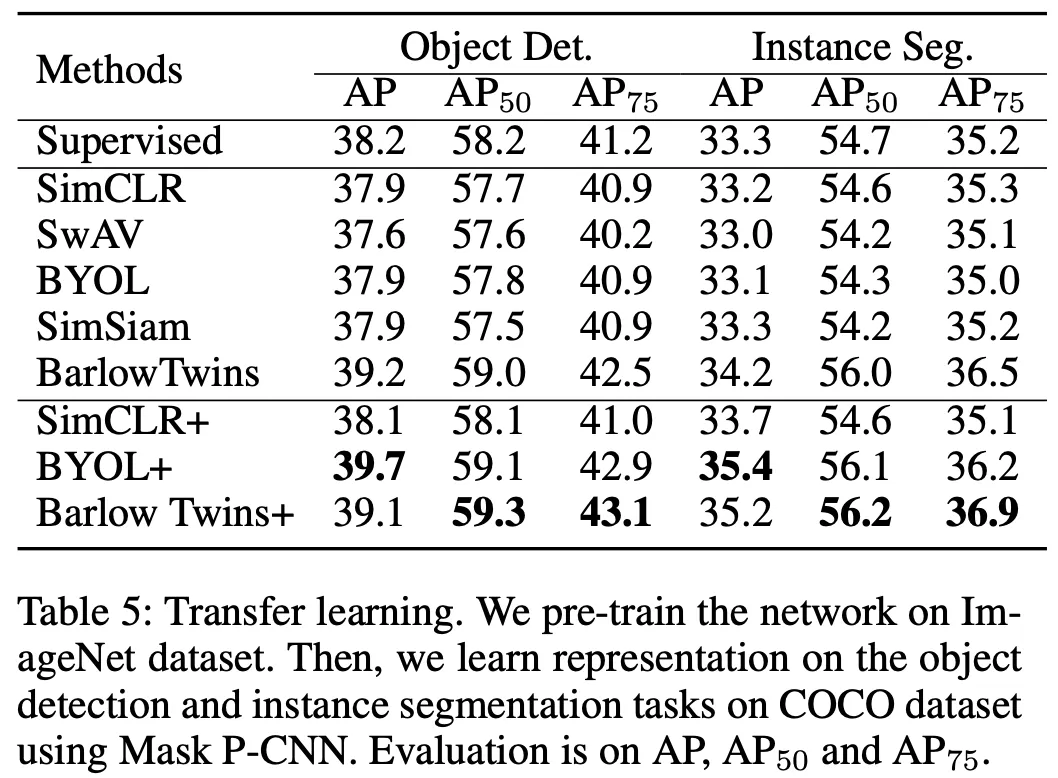
Experiment