MASKED FREQUENCY MODELING FOR SELF-SUPERVISED VISUAL PRE-TRAINING

ICLR 2023 Accepted Paper

Link: https://github.com/Jiahao000/MFM

 

Summary

• MFM Approach
  • Masks a portion of the input image's frequency components.
  • Predicts the missing frequencies in the frequency spectrum.
• Key Insight
  • Predicting masked components in the frequency domain better reveals underlying image patterns than predicting masked patches in the spatial domain.
  • The frequency domain is more effective due to high spatial redundancy.
• Mask-and-Predict Strategy
  • With the appropriate configuration:
    • Utilizes structural information within high-frequency components.
    • Leverages low-level statistics among low-frequency components.
  • Facilitates effective representation learning.
• Framework Features
  • Employs a simple non-Siamese architecture.
  • Does not use:
    • Extra data
    • Extra models
    • Mask tokens
• Experimental Results
  • Demonstrates competitive performance in image classification and semantic segmentation tasks.
  • Achieves advanced robustness across various benchmarks.
  • Outperforms recent masked image modeling approaches in both performance and robustness.

Introduction or Motivation

• interested in investigating the effectiveness of other corruption strategies for self-supervised representation learning.
• first explore the corruption recipes commonly applied in low-level image processing tasks
  • including image super-resolution (SR), deblurring, and denoising.
• Corruptions induced in the spatial domain prevent us from analyzing what specific information is corrupted and needs to be reconstructed.
• To better understand these low-level corruptions, we shift our attention from the spatial image domain to the frequency domain.

Method

Overview

1. perform Fast Fourier Transform (FFT) to convert each input image into its frequency representation
2. mask a portion of frequencies on the frequency spectrum using a low-/high-pass filter.
3. With inverse FFT (iFFT), we finally take the corrupted image with some of the frequencies attenuated as input.
4. Our decoder is a lightweight linear layer that reconstructs the masked frequency values on the frequency spectrum via a frequency loss.

Reconstruction Target

def loss_formulation(self, recon_freq, real_freq, matrix=None):
    # frequency distance using (squared) Euclidean distance
    tmp = (recon_freq - real_freq) ** 2
    loss = torch.sqrt(tmp[..., 0] + tmp[..., 1] + 1e-12) ** self.loss_gamma
    if self.with_matrix:
        # spectrum weight matrix
        if matrix is not None:
            # if the matrix is predefined
            weight_matrix = matrix.detach()
        else:
            # if the matrix is calculated online: continuous, dynamic, based on current Euclidean distance
            matrix_tmp = (recon_freq - real_freq) ** 2
            matrix_tmp = torch.sqrt(matrix_tmp[..., 0] + matrix_tmp[..., 1]) ** self.matrix_gamma

            # whether to adjust the spectrum weight matrix by logarithm
            if self.log_matrix:
                matrix_tmp = torch.log(matrix_tmp + 1.0)

            # whether to calculate the spectrum weight matrix using batch-based statistics
            if self.batch_matrix:
                matrix_tmp = matrix_tmp / matrix_tmp.max()
            else:
                matrix_tmp = matrix_tmp / matrix_tmp.max(-1).values.max(-1).values[:, :, :, None, None]

            matrix_tmp[torch.isnan(matrix_tmp)] = 0.0
            matrix_tmp = torch.clamp(matrix_tmp, min=0.0, max=1.0)
            weight_matrix = matrix_tmp.clone().detach()

        assert weight_matrix.min().item() >= 0 and weight_matrix.max().item() <= 1, (
            'The values of spectrum weight matrix should be in the range [0, 1], '
            'but got Min: %.10f Max: %.10f' % (weight_matrix.min().item(), weight_matrix.max().item()))
        # dynamic spectrum weighting (Hadamard product)
        loss = weight_matrix * loss
    return loss

Experiment

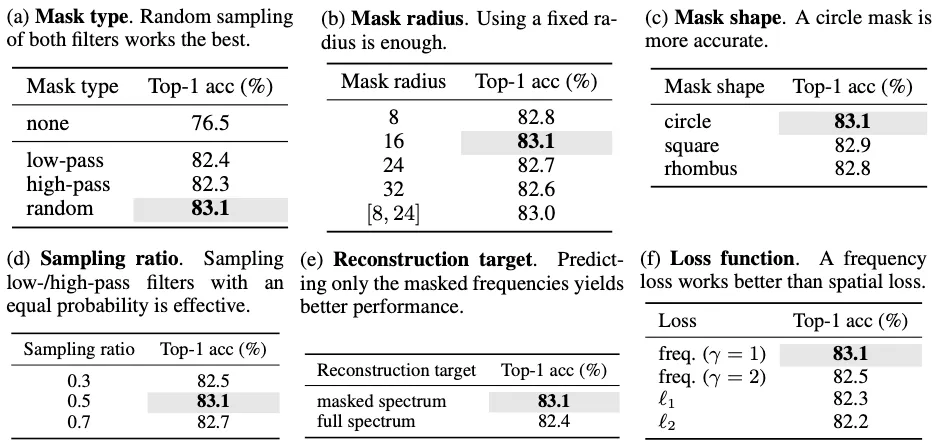
• Importance of Hyperparameters
  • Finding the right hyperparameters is crucial.
• Decoder Design Choice
  • Opted for a linear layer instead of an 8-layer decoder because a linear layer alone appears sufficient.
• Training Speed and Scalability
  • The architecture is inherently slower than MAE in terms of overall training speed.
  • Training was generally limited to ViT-B, indicating that larger models may face diminishing returns as their drawbacks outweigh the benefits.
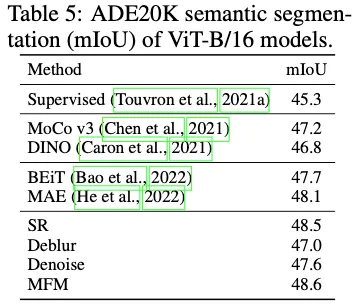
• Performance Comparison with Existing Models
  • Compared to CrossMAE and FastConvMAE, MFM delivers comparable performance for smaller models.
  • However, as model size increases, MFM becomes less attractive due to slower training speeds and scalability issues.