ECCV 2024 Accepted Paper
Link: https://arxiv.org/pdf/2404.08351
Summary
- 코드를 뜯어서 이해를 해야하는데 그 부분이 어렵다.
- 완벽하게 dataset이 geo-referencing을 활용해 align이 되어있다면 spatial multi-modalities를 살려서 이것저것 해볼 수 있는 것들이 많다.
- 방법론 자체가 omni 방식의 MAE이긴 하지만 새롭거나 하지는 않았다.
Introduction or Motivation
Limitations
Despite this potential, most multimodal EO datasets and models focus on a single data type, either mono-date images or time series. This limitation prevents them from simultaneously leveraging the spatial resolution of aerial images, the temporal and spectral resolutions of optical satellite time series, and the resilience of radar to weather effects. Additionally, existing approaches are often limited for a given set of sensors, limiting their applicability.
Suggested Solution
To address these challenges, we introduce OmniSat, a novel architecture designed for the self-supervised fusion of diverse EO data. Existing multimodal approaches often map multiple unrelated observations from different modalities to one pivot modality or a shared latent space.
OmniSat merges multiple views of the same area from different modalities into a single representation combining the specific information of each modality
Contributions
- combine varied sources of EO observations in a self-supervised manner, resulting in richer joint representations that capture the unique characteristics of each modality.
- augment two EO benchmarks to create the first datasets with three modalities of different natures (very high resolution images, optical and SAR time series).
Method

Two Commonly used EO benchmark dataset
- TreeSatAI
- PASTIS-R
→ focus on crop type mapping and forestry differs from the land cover analysis of FLAIR
$x$: a tole observed through a set $\text{M}$ of $M$ distinct sensors or modalities.
The goal of the OmniSat model is to learn in a self-supervised fashion to combine all modalities M into a multimodal representation $f^*$
Multimodal Tokenization
- All available modalities are spatially aligned through georeferencing.
- 때문에 tile을 non-overlapping patch $$ $P \in \text{P}$로 나눠도 align이 여전히 맞는다.
- $x_p^{\text{M}}=\{x_p^m\}_{m\in\text{M}}$ corresponds to $M$ distinct views of the same patch $p$ with different modalities.
- Each modality $m$ takes its values in a space $\Omega^m$ such tha $x_p^m\in\Omega^m$
- Index tokens with pairs $(m, p)$
Encoder-Decoder for Images
- Encode these inputs with a sequence of convolutions and max-pool layers until the spatial dimension is fully collapsed.
- Decoding involves a symmetric sequence of convolutions and un-pooling layers.
- pass the pooling indices from the encoder’s max-pooling to the decoder’s un-pooling in the manner of SegNet
Encoder-Decoder for Time Series
- $Ω^{TS}=\mathbb{R}^{C \times L}$
- Encode the temporal patches using a Lightweight Temporal Attention Encoder (LTAE)
- Encoded feature를 L만큼 repeat해서 $\mathbb{R}^{C\times L}$로 맞추기
- 하지만 decoder는 어떤게 cloudy하고 rainy한지는 알 수 없기 때문에 LTAE의 temporal attention maps 중에서 상위 25%를 대상에게만 reconstruction loss를 적용
Modality Combining Network
- $M \times P$개의 tokens에 대해서 각각의 위치에 맞춰 Euclidean relative positional encoding을 수행
- horizontal transform 의해 변하지 않기 때문에, absolute positional encoding 대신 relative positional encoding을 사용하는 것이 더 바람직
- 아래의 수식을 통해서 all available modalities를 encoding한다
- $g_\text{P}^{\text{M}}=\text{self-attention}(f_\text{P}^{\text{M}};r)$
- $f_\text{P}^{\text{*}}=\text{cross-attention}(f_\text{P}^{\text{comb}};g_\text{P}^{\text{M}};r)$
- 여기서 $f_\text{P}^{\text{comb}}$는 learnable parameter
→ 모델의 학습 흐름을 코드로 확인하고 싶었지만 Hydra 및 Lightning 기반으로 코드가 작성되어서 이해할 수가 없었다…
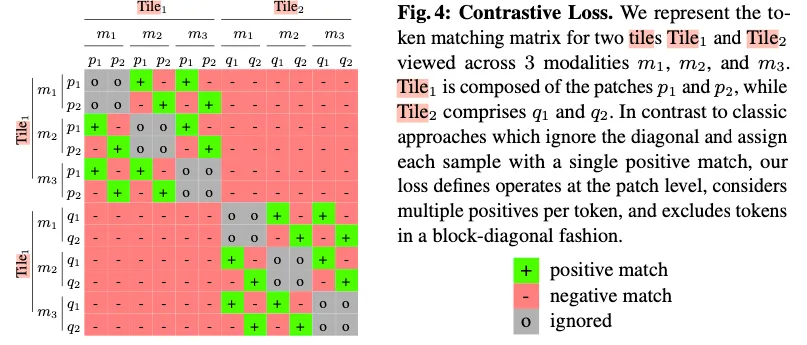
Contrastive Objective
- 다른 modalities간에는 가까워지고, 다른 patches간에는 가까워지고 싶지는 않다(영향 x)
- closer: $(f_p^m,f_p^n)$ for not $n \ne m$,
- Positive: 동일한 patch에 대해서 모달리티가 다른 경우
- Negative: EO에서 가까운 patch는 시각적으로 비슷하기 때문에 동일한 modality에 있는 아주 가까운 patch는 negative sample에서 제외 → $M \times B \setminus T(m, p)$ where $B$ is set of current visible patches
Multimodal Reconstruction Objective

- mask a fraction of tokens: $\mathbf{K}\subset \mathbf{M} \times \mathbf{P}$
- $f_P^\star = \mathcal{C} \left( \{f_p^m \}{(m,p) \notin \mathcal{K}} \cup \{f_p^{\text{mask}} \}{(m,p) \in \mathcal{K}} \right)$
- $\mathcal{L}{\text{reconstr}} = \frac{1}{|\mathcal{K}|} \sum{(m,p) \in \mathcal{K}} \frac{1}{\dim(\Omega^m)} \left\| \mathcal{D}^m(f_P^\star) - x_p^m \right\|^2$
Experiment