Inception Transformer

NeurIPS 2022 Accepted Paper

Link: https://arxiv.org/abs/2205.12956

 

Summary

• Transformer는 long-range dependencies 구축에는 강하지만 local information을 잘 전달하는 high frequency를 capturing하는데에는 약하다.
• 그래서 high and low frequency를 모두 잘 잡을 수 있도록 inception mixer를 도입한다.

Introduction or Motivation

• ViT and its variants are highly capable of capturing low-frequencies in the visual data
  • Global shapes and structures of a scene or object
• But not very powerful for learning high-frequencies, mainly including local edges and textures.
  • ViT의 self-attention은 global operation이기 때문에 global information(low-frequency)를 capturing하는데에 더 유리
• ViT’s Low-frequency preferability → ViT’s performance down
  1. low-frequency information filling in all the layers may deteriorate high-frequency component
     • local textures, and weakens modeling capability of ViTs
  2. high-frequency information is also discriminative and can benefit many tasks
     • (fine-grained) classification
• Hence, it is necessary to develop a new ViT architecture for capturing both high and low frequencies in the visual data.

Inception Mixer

• Aims to augment the perception capability of ViTs in the frequency spectrum by capturing both high and low frequencies in the data.
  • Split components into high-frequency mixer and low-frequency
  • High-frequency mixer consists of a max-pooling operation and a parallel convolution operation
  • Low-frequency mixer is implemented by a vanilla self-attention in ViTs

Moreover, we find that lower layers often need more local information, while higher layers desire more global information

Frequency Ramp Structure

• From lower to higher layers, gradually feed more channel dimensions to low-frequency mixer and fewer channel

Method

• Given Feature $\mathbf{X} \in \mathbb{R}^{N \times C}$ split it into $\mathbf{X}_h \in \mathbb{R}^{N \times C_h}$ and $\mathbf{X}_l \in \mathbb{R}^{N \times C_l}$
  • where $C_h + C_l = C$
  • $\mathbf{X}_h$ : High-frequency
  • $\mathbf{X}_l$ : Low-frequency
• Divide the input $\mathbf{X}h$ into $\mathbf{X}{h_1} \in \mathbb{R}^{N \times \frac{C_h}{2}}$ and $\mathbf{X}_{h_2} \in \mathbb{R}^{N \times \frac{C_h}{2}}$

 

High-frequency Mixer

• $\mathbf{Y}{h_1} = \text{FC}(\text{MaxPool}(\mathbf{X}{h_1}))$
• $\mathbf{Y}{h_2} = \text{DwConv}(\text{FC}(\mathbf{X}{h_2}))$
• $\mathbf{Y}_l = \text{Upsample}(\text{MSA}(\text{AvePooling}(\mathbf{X}_l)))$s
• $\mathbf{Y}c = \text{Concat}(\mathbf{Y}l, \mathbf{Y}{h_1}, \mathbf{Y}{h_2})$
• $\mathbf{Y} = \text{FC}(\mathbf{Y}_c + \text{DwConv}(\mathbf{Y}_c))$
• $\mathbf{Y}=\mathbf{X} + \text{ITM}(\text{LN}(\mathbf{X}))$, Inception Token Mixer
• $\mathbf{H}=\mathbf{Y} + \text{ITM}(\text{LN}(\mathbf{Y}))$

 

Frequency Ramp Sturcture

• Gradually splits more channel dimensions from lower to higher layers to low-frequency mixer
• Leave fewer channel dimensions to high-frequency mixer

$\mathbf{Y}_l = \text{Upsample}(\text{MSA}(\text{AvePooling}(\mathbf{X}_l)))$

 

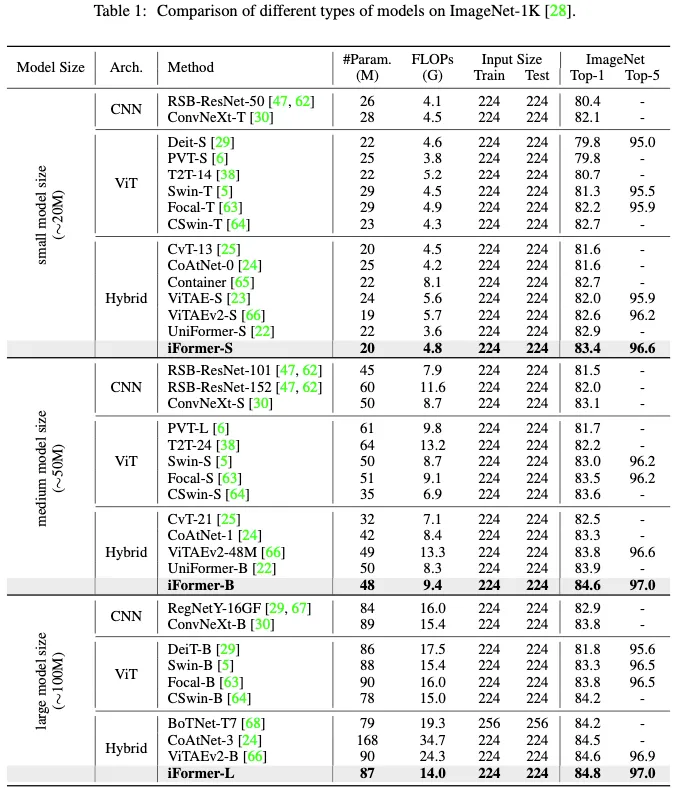
Experiment

Limitations

• Requires manually defined channel ratio in the frequency ramp structure